So I've been sitting on this paper for a few weeks now. Wanted to stew over these results for a while. Honestly, at this point I can't tell if this is an elaborate larp by ChatGPT/Claude or what. It's definitely a bizarre feeling trying to become an expert on a theory that isn't really fleshed outeven to the point where you don't fully understand parts of it yourself.
That said, 80% of what I said has held true since that original speed of light paper release. Where I went wrong was circular reasoning for the growth law, where I was trying to falsify each law based on the Lorentz equation. Anyway, putting that behind me and moving on.
I did a couple things back in June. First, I realized that I was incorrectly thinking of entanglement in terms of localitythat Earth was in its own entanglement field and had our own local speed of light. But that's not really what's happening when we look at this telescope data.
Assuming S Theory is right and the speed of light is a function of the entanglement level, we are seeing a historical record of the speed of light over time. I had Claude look up 20 random galaxies spanning from z = 1 to z = 14. I used the lookback time to normalize them all to my definition of entropic time (t_normal=temit/t_total). That is, t = 0 is the Big Bang and t = 13.8 billion years is today.
When I do that, I get this graph when I assume redshift is from varying speed of light. That was cool. Didn't know what it meant, but when I curve fit it I got a power law with an R2 value of 0.994, which is surprisingly tight. It also gives me some nice falsifiable evidence. If it's right, as we keep looking back further in time, we'll see more red shift. Curious to see what it looks like as we look deeper and deeper whether this power law holds.
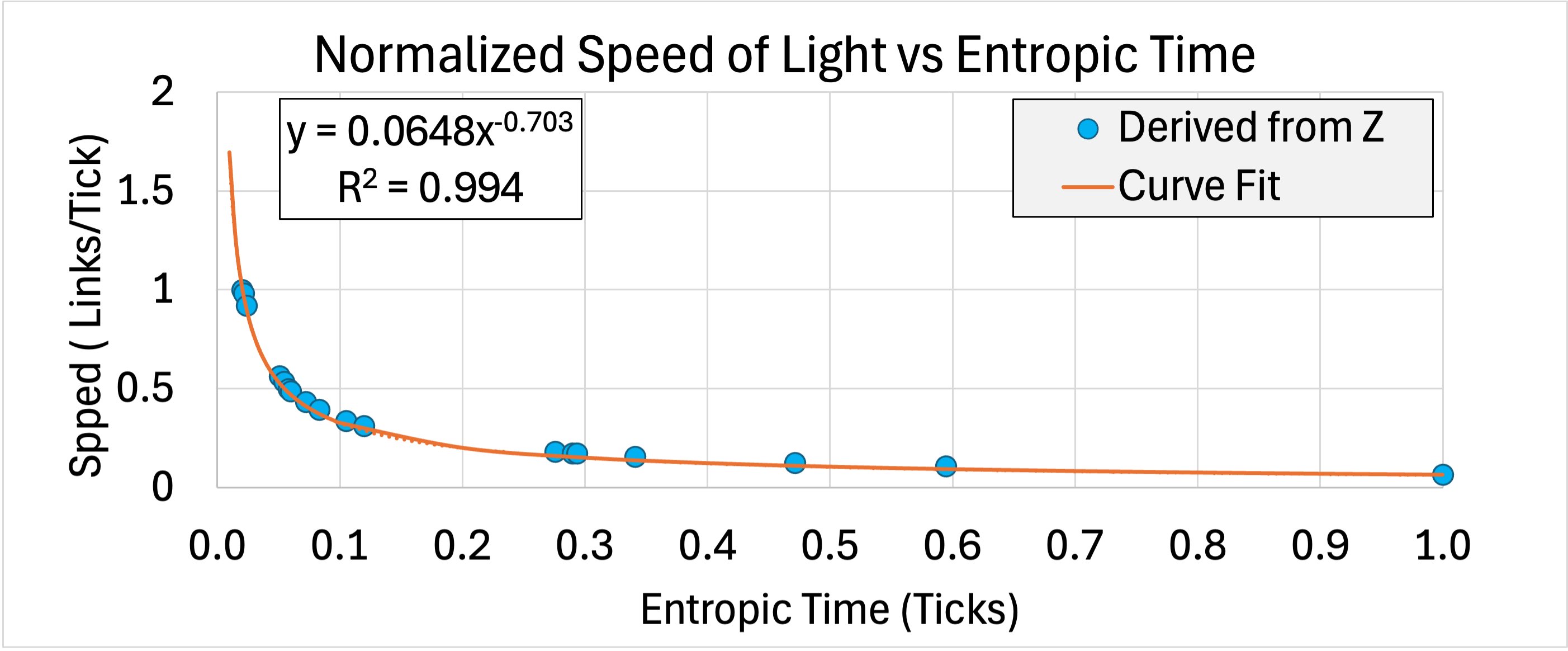
The first thing I looked into was how long it would take to see a measurable difference in the speed of light. Where we are in the SOL curve suggests with would take something like 3 million years before we can detect it. So come back in 3 million years and we'll see if I was right.
Then I thought back to my photon propagation simulation where the photon changed speeds in varying S_{ij} fields. Seems obvious to me now that dS/dt is the normalized speed of light. At the time of the very first white paper, I'd written it as eta*smax, not really considering the option that the speed of light might change over time.
Anyway, if I take the integral of this speed-of-light curve, I get the cumulative S over the entire history of the universe, and that lets me calculate current S based on measured data. That puts S_{ij} = 0.218 at t = 1. Again, wasn't sure what to do with this, but it felt a lot more pure mathematically than what I was doing before.
Next, I started thinking about the growth law. If S Theory is to be a unifying theory, it needs to work with quantum mechanics and black holes. I spent a little time tinkering with Schwarzschild's equations and determined that the (1 - S_{ij}) term really should be (1 - S_{ij})^2 to get the curvature leading up to the event horizon correct. That brought me to:
dS/dt=eta*(1-S)^2
So what's eta? The normalized speed of light curve is clearly a power law, so I decided eta must be of the form S_{ij}^{-\beta} for it to work. Okay, so what's beta? Well, based on combinatorics in the early universe and the probability of stable triangles forming, it forced beta = 2.
Also decided I needed some scaling factor. I called it alpha, and the growth law became:
dS/dt=alpha*S^(-2)*(1-S)^2
Now, I take all this telescope data and plug it into my photon SEM model. First, I place nodes at each of the galaxies and space them out according to their distance, calculated based on the normalized speed of light. I inject photon SEMs on a time delay at each of the galaxies and let them propagate toward Earth, and allow the growth law to run. Entanglement increases over time while light is propagating towards earth. There's a bend to it and all the sources arrive precisely when they mean to.
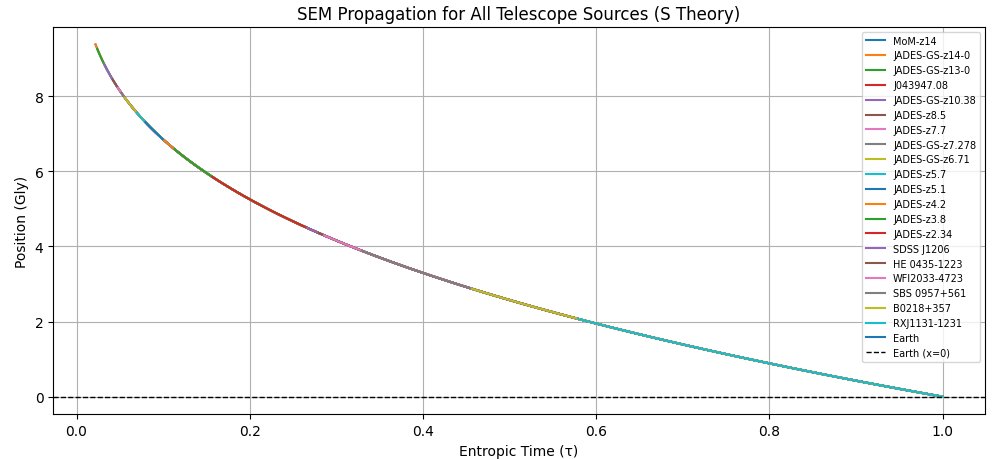
The one free parameter I have at this point is alpha. The best results I got came from alpha = 0.00447, so I just rounded it to 0.005 and set it as the official growth law. This ordinary differential equation predicts distant galaxy redshifts within 5% and does so without dark energy or expansion. Alpha=.005 must have some physical meaning, but I haven't found it yet. Chatgpt thinks it has something to do with the number of available SEM configurations. I have my doubts and have set it aside for now and am just shrugging my shoulders.
Annoyingly, closer galaxies don't line up quite as well from a raw percentage standpoint, but I suspect that has to do with their actual velocities coming into play....that and I'm dividing by a small number already.
I kept some of the data I pulled from this training set and used it as a check after setting alpha = 0.005. Here are the results. I don't know. Maybe it's just elegant curve fitting.
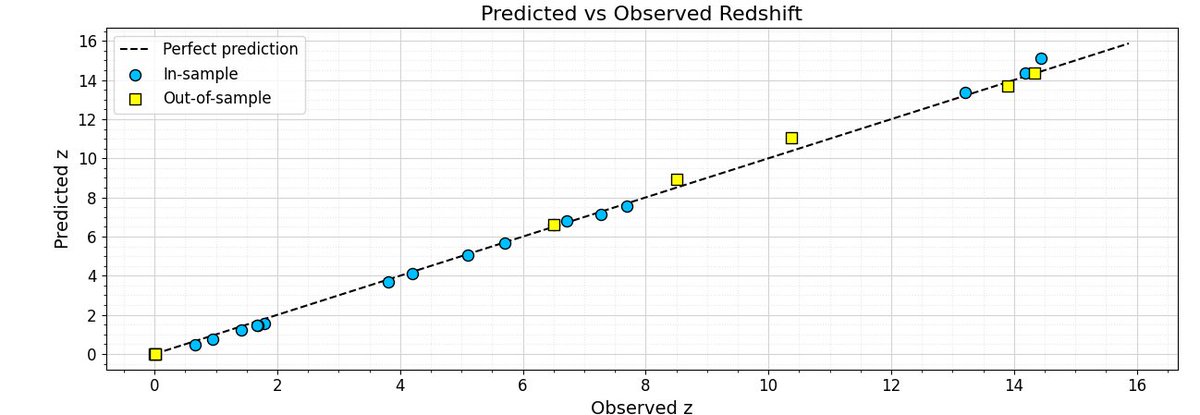
Right now, I have 24 data sets. In the future, I plan to expand this to several thousand if I find the free time. I think that would be telling as well.
Here's where it gets a little interesting. Now that I have this growth law, I can go back and calculate when the cosmic microwave background happened based on the first acoustic peak. I'm showing that happened around 13k years after the Big Bang. Initially, I said "WTF, it should be 380k after the Big Bang. This is garbage."
Part of me dragging my feet on this paper has been trying to get Big Bang nucleosynthesis and the acoustic peaks right. If I assume T_yr=31,500K that also lines up with 13Kyr. None of this seemed right until I went and calculated what a fast speed of light during this timeline meant, and I showed that within this 13k years,
340 million years of local time passed. So galaxies had 340 million years to form compared to CDM's 380k years. If S Theory is to be believed, this explains why we are seeing galaxies when we shouldn't.
I'm a long way away from that though, since I have to deal with some of the thermodynamics of BBN more formally than I have been. In order to even start that, I need to be able to calculate units of stuff. At this point, I decided I needed an anchor for my growth law and set present-day speed of light = dS/dt @ S = 0.218. This allows me to calculate length from how long it takes for my photon to travel from one point to the next. Gives me energy in Joules, and based on energy, lets me calculate massall in SI units. That's pretty cool I guess.
Next up: WTF do I do about electrical properties? I decided that the fundamental unit of charge comes from the electron, so I need to find the first SEM that gives me the right spin, mass, and quantized charge of an electron. Turns out, my electron is a 23-node SEM, and all of a sudden I can calculate electrical units. Assuming of course, it is an electron.
From here, I can get Maxwell's equations, and just for the fun of it, I can show Lorentz invariants.
Again, I'm not even convinced of all this. I don't personally like that the electron takes 23 nodes to show up, and I'm not sure I can articulate why. What I think needs to happen is for the constraints that produce these particles to somehow be eigenstates of the entanglement field. Like in real life, all ~10^80 electrons in the universe are exactly the same, so there must be some entanglement state that stabilizes at that exact configuration and does it every time. Quite the interesting problem right there. The constraint matrix I have just feels too complicated to be right. Too many miracles would have to happen to get this exact constraint combination:
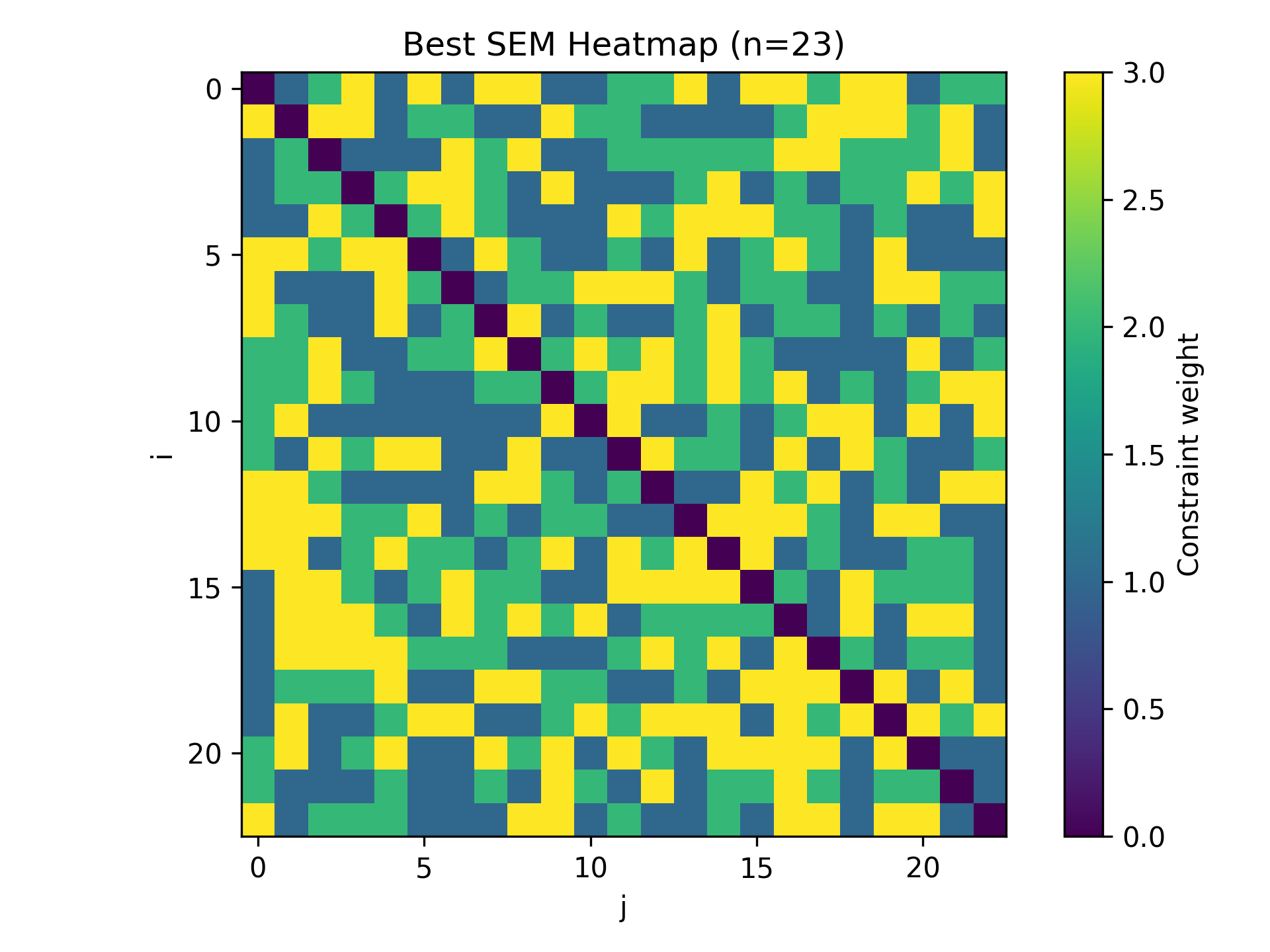
Next up on my list: I gotta get my quantum zoo sorted. And part of this is solving the higgs field. I believe I have the higgs field already accounted for in my lagrangian. It appears part of the asymmetric constraint equation that's responsible for mass. If I can show that eigenstates result in known particles, then I'll dust off the mantel for my future Nobel Prize. That's certainly not going to happen over night. Until then, I'll keep plugging along on my free time. . I'll post the latest paper revision shortly.









